先日、このようなツイートを書いたところ、かなりの反響がありました。

JavaScript の正規表現の脆弱性の例でいうと、例えば /\s+$/ は脆弱性があると言える

console.time();
/\s+$/.test(" ".repeat(65536) + "a");
console.timeEnd();

結構時間がかかるのがわかる。でも /\s+$/ を見て「これは危険だな」と理解出来る人はそんなにいない。JavaScript に限らないけれど。

— Takuo Kihira (@tkihira) February 17, 2022

これは一般に ReDoS (Regular expression Denial of Service) と呼ばれる脆弱性です。正確に理解するのが難しい脆弱性なので、少し解説してみたいと思います。

結論

長い記事になるので、最初に「とりあえずこれだけ知っておけば良かろう」という点をまとめておきます。

プログラミング言語の問題ではなく、正規表現エンジンの実装依存で発生する問題である

言語（JavaScript）の問題ではなく、言語の実行環境で採用している正規表現を処理するエンジンの実装の問題です。Perl でも Python でも Go でも、その環境の正規表現エンジンの実装次第で発生しうる問題です。

正規表現の形から問題の発生を想像するのは、とてもむずかしい

後戻りしない形の正規表現であれば発生しないのですが、正規表現の形から発生の可能性を正確に判断するのは至難の業ですし、そもそも同じ正規表現であっても後戻りするかどうかは正規表現エンジンの実装に左右されることもあります。

入力文字数が短くても発生しうる

例えば、 /(.*){1,20}[bc]/.exec('a'.repeat(25)) のように、入力文字がたったの 25 文字でも物凄く遅くなり得ます。正規表現エンジンの実装次第ですが、基本的に入力文字数の制限は本質的な解決にはなりません（なお後述しますが、例えば Go の標準の正規表現エンジンの実装では、正規表現の長さを m、入力文字を n として計算量が O(mn) となるため、入力文字数の制限が本質的な解決になることもあります）

タイムアウトでプロセスを殺すのが一番確実

脆弱性とはいえ、攻撃によって内部に侵入される系のものではなく、無限ループが発生する程度の脆弱性ではあります。適切なタイムアウトを指定してプロセスを殺す運用が可能であれば、大抵のサービスにおいてそれほど神経質にならなくても良いでしょう。

もちろん発生させないのが一番なのですが、正規表現を使う以上根絶の難しい問題でもあります。かといって正規表現を一切使わないという判断も極端であると思うので、ReDoS の存在を知っておいて、発生したときに「あ〜ReDoS が発生しているね」と気付ける程度で良いのではないかと思います。

ではここからは、なぜこのような問題が起こるのか、どのようにそれを防ぐのかについて解説しましょう。

一体何が起こっているのか

オリジナルの問題にもどって考えてみましょう。ツイートの正規表現を少しだけ変えました。

/a*z/.exec('a'.repeat(65535) + 'b')

よくある正規表現エンジンでは、まずこの aaaa...aaab という文字列の先頭からマッチングを開始します。a* には aaa… がどこまでもマッチングするので、65535 個の a にマッチした後、最後の b に出会います。残念ながら最後の文字は z でなくてはいけないので、せっかく 65536 回も比較したのに、このマッチングは失敗です。

次に、文字列の 2 文字目から同じ処理を開始します。同じように、今度は 65534 個の a にマッチした後、最後の b に出会って、同じように失敗します。今回は 65535 回の比較をしたにも関わらず失敗です。

これが延々と続いていきます。最終的には、65536 文字の入力に対して、(65536 + 65535 + 65534 + … + 3 + 2 + 1) 回の比較が発生します。総比較回数は (1 + 65536) * 65536 / 2 === 2,147,516,416 回、約 21 億回もの比較が発生してしまっているのです。計算量でいうと、入力文字を n とすると O(n^2) ですね。

このように、繰り返しが何度も発生する正規表現に対して外部から重くなる入力を与えられることでサービスが落ちるタイプの脆弱性を ReDoS (Regular expression Denial of Service) と呼びます。

これは割とよく知られた問題なので、一部の正規表現エンジンの実装ではこういった典型的なパターンに対して、「最後に登場する文字が入力文字列にない場合は失敗と判断する」といった枝切りを入れて対応している場合もあります。例えば手元の perl で上記の実行した例はこちらですが、一瞬で終了しております。

$ time perl -e '("a" x 65535) =~ /a*z/'

real	0m0.013s
user	0m0.002s
sys	0m0.007s

しかし、これは本質的な解決策ではないため、例えばちょっと正規表現に手を加えるだけで枝切りに失敗して同じように計算量が膨れ上がってしまいます。

$ time perl -e '("a" x 65535) =~ /a*[yz]/'

real	0m19.003s
user	0m18.854s
sys	0m0.134s

このように、正規表現エンジンの内部実装によって発生状況が大きく左右されるので、ReDoS に対して「この言語なら大丈夫」みたいな理解をしていると危険です。

なお、実は今回の正規表現における計算量の増大はマシな方で、例えば次のような例の場合は O(2^n) のオーダーで計算量が爆発します。原理は同じで、比較に失敗した場合に後ろに戻らなければいけないのが原因です。

const test = (n) => {
  const strexp = "a?".repeat(n) + "a".repeat(n);
  const regexp = new RegExp(strexp); // n:5 => /a?a?a?a?a?aaaaa/
  console.time();
  regexp.exec("a".repeat(n));
  console.timeEnd();
};
test(50);

正規表現エンジンの内部実装

もっと正確に原因を理解するためには、正規表現エンジンの内部実装について理解する必要があります。大変複雑な話になるので、ここでは軽くさわりだけ説明しましょう。それでも結構な長文になるので、対策だけ知りたい！という方は「対策」まで飛ばしてください。

正規表現を有向グラフで表現する

正規表現は、エンジン内部では一般的に有向グラフで表現されます。例えば az というシンプルな正規表現は、次のようなグラフで表されます。

[スタート] -(a)-> [状態1] -(z)-> [ゴール]

辺に書かれている文字は、「この文字が入力ならば、この辺を使って遷移してよい」というルールです。acaz という文字列を az という正規表現で検索する例で考えてみましょう。

• まず 1 文字目は a なので、スタートから状態 1 に遷移出来ます。2 文字目は c なので、状態1 から遷移出来ないので失敗です
• 次に 2 文字目から再度スタートします。2 文字目は c なので、スタートの状態から遷移出来ないので、早くも失敗です。
• その次は 3 文字目からスタートです。3 文字目は a なので、状態 1 に遷移します。次の 4 文字目 z は、状態 1 からゴールの遷移が出来ます。よってゴールの状態に到着し、検索成功です。

この例だとあまりに単純でした。では次に a*z という正規表現について考えてみましょう

   |------------(z)-------------|
   |                            v
[スタート] --(a)-> [状態 1]    [ゴール]
   ^                 |
   |-------(ε)-------|

ここで、謎の「ε（イプシロン）」という遷移が出てきました。これは「無条件で遷移してオッケー！」というルールです。スタートの状態で a を受け取ると状態 1 に遷移するのですが、そこから ε 遷移を利用して無条件にスタートの状態に戻れます。よって、スタートの状態では何個でも a を受け取ることが出来ます。一方でスタート状態で z を受け取るとゴールに遷移し、検索が成功します。このように、検索中に入力文字に応じて状態を遷移させながら、最終的にゴールにたどり着いたら成功、たどり着けなければ失敗となります。

なお、同じ検索を表現するグラフは複数存在します。例えば次のようなグラフも同じ a*z の検索が可能です。

   |-----------------(z)------------------------|
   |                                            v
[スタート] --(ε)-> [状態 1] --(ε)-> [状態 2]    [ゴール]
   ^                                 |
   |-------------(a)-----------------|

遷移先が 1 つに定まらないことがある

今までは比較的シンプルな例を使ってきましたが、少し複雑な正規表現で考えてみましょう。複雑な例として、a?a?aa という正規表現を考えましょう。言葉にすると、「aa」「aaa」「aaaa」のどれかにマッチする正規表現になります。

[スタート] --(a)-> [状態 1] --(a)-> [状態 2] --(a)-> [状態 3] --(a)-> [ゴール]
   |                ^ |              ^
   |------(ε)-------| |------(ε)-----|

ε 遷移を使うと、このような形で有向グラフで表現出来ます。ここで aa を入力とした場合にどのように検索されるか考えてみましょう。

• まずスタートで入力 1 文字目の a を受け取り、状態 1 に遷移します。次に状態 1 で入力 2 文字目の a を受け取り、状態 2 に遷移します。入力はここで終了のため、ここでの検索は失敗です。
• そこで、1 つ前の状態 1 に戻って、そこで ε 遷移を使って状態 2 に遷移します。そこで入力 2 文字目の a を受け取り、状態 3 に遷移します。しかし入力はここで終了のため、この検索も失敗です。
• そこでさらに 1 つ前の状態、すなわちスタート状態に戻り、ここで ε 遷移を使って状態 1 に移動します。状態 1 で入力 1 文字目の a を受け取り状態 2 に遷移し、状態 2 で 2 文字目の a を受け取り状態 3 に遷移します。しかしここで入力文字はなくなるため、この検索も失敗です。
• そこで直前の検索の状態 1 まで戻り、ここで ε 遷移を使って状態 2 に移動します。状態 2 で入力 1 文字目の a を受け取り状態 3 に遷移し、状態 3 で入力 2 文字目の a を受け取りゴールに遷移し、やっと成功です。

このように、深さ優先探索で検索をすると、絵に描いたようなバックトラックの最悪パターンが発生し、何度も何度も後戻りが発生してしまいます。今回は 2 文字の aa だったのでまだ手で書く気になれましたが、a?a?a?a?aaaa に対する aaaa の検索とかになると、もう手では追いたくないレベルで複雑になってしまいます。この「後戻り」というのがポイントで、この後戻りが頻繁に発生すると正規表現の検索コストが跳ね上がってしまいます。

このように ε 遷移があると、入力文字が 1 文字送られてきても次の遷移先がどこなのか 1 つに定まらないため、総当たりで全通り試す必要が出てしまいます。この 1 つに定まらない状態を英語で “Nondeterministic” と呼びます。そして、今回の有向グラフのような状態と遷移の組み合わせをオートマトン（automaton）と呼びます。今回は有限個（finite）なので有限オートマトン、かつ入力に応じて遷移先が必ずしも定まらないので非決定性有限オートマトン（Nondeterministic Finite Automaton、NFA）と呼びます。

どのような正規表現であっても、必ず対応する非決定性有限オートマトン（NFA）を作り出すことが出来ることが数学的に証明されています。興味のある方は、計算理論の基礎を読んでみましょう。

遷移先を 1 つに定めることが出来る

これに対応して、遷移先が必ず 1 つに定まる有向グラフが存在します。 a?a?aa に対して次のような有向グラフを考えてみましょう。

[スタート] --(a)-> [状態 1] --(a)-> [状態 2（ゴール）] --(a)-> [状態 3（ゴール）] --(a)-> [ゴール]

ゴールが 3 つありますが、とりあえずそれを無視して遷移だけ見てみましょう。ε 遷移がなく、どの状態においても特定の入力文字に対して遷移先が必ず 1 つである（もしくは遷移先がない）ことが保証されています。このような形の状態と遷移の組み合わせ（オートマトン）であると、後戻りさせて再度別のルートを試す必要は絶対に発生しません。ただ機械的に、入力文字に応じて状態を遷移させるだけになります。

先程と同じように aa を入力文字として考えてみましょう。スタートで 1 文字目の a を受け取って状態 1 に遷移し、そこで 2 文字目の a を受け取って状態 2 に遷移します。そして最後の入力文字を受け付けた時にその遷移先の状態がゴールであれば、検索は成功したと考えます。今回は状態 2 がゴールですので、この検索は成功です。

このように、遷移先が必ず 1 つであることが保証されている場合、検索は入力文字数を n として O(n) の計算量で終わります。ものすごく速いですね。入力に応じて遷移先の状態が必ず 1 つに定まることを英語で “Deterministic” と表現し、このようなオートマトンのことを決定性有限オートマトン（Deterministic Finite Automaton、DFA）と呼びます。

そしてなんと、NFA から DFA に自動的に変換することが常に可能であることが数学的に証明されています。興味のある方は、計算理論の基礎を読んでみましょう。

現実的に正規表現エンジンで利用されているのは NFA

DFA を構築することが出来れば O(n) で検索出来るのであれば、可能な限り DFA を構築したいですよね。そして正規表現から NFA は自動的に生成可能であり、NFA から DFA も自動的に生成可能であるならば、正規表現から DFA に変換しない理由なんてない、と思われるかもしれません。ところが残念ながら、そう簡単な話ではありません。DFA の変換において、状態遷移数が簡単に爆発してしまう可能性があるのです。

例えば、簡単な正規表現 (a|b|c|d|e)+ から DFA を構築することを考えてみましょう。スタート（初期状態といいます）が受け取る文字列は a b c d e の 5 種類で、それぞれの遷移先を状態 a、状態 b、状態 c、状態 d、状態 e の 5 つになるでしょう。それぞれがゴール（受理状態といいます）になります。状態数としては、これで全てで良いでしょう。問題は遷移です。

状態 a では、再度 a b c d e の 5 種類の入力を受けることが出来ます。状態 a で a を受け取ったら自分自身（状態 a）に遷移し、b を受け取ったら状態 b に遷移し…、と状態 a からは 5 本の遷移が出るであろうことが想像されます。

同様に、状態 b からも 5 本、状態 c からも 5 本…と遷移が出るので、最終的には全ての状態から全ての状態に遷移の線が発生し、 5 * 5 = 25 本の遷移が発生します。絵にするとこんな感じですね。

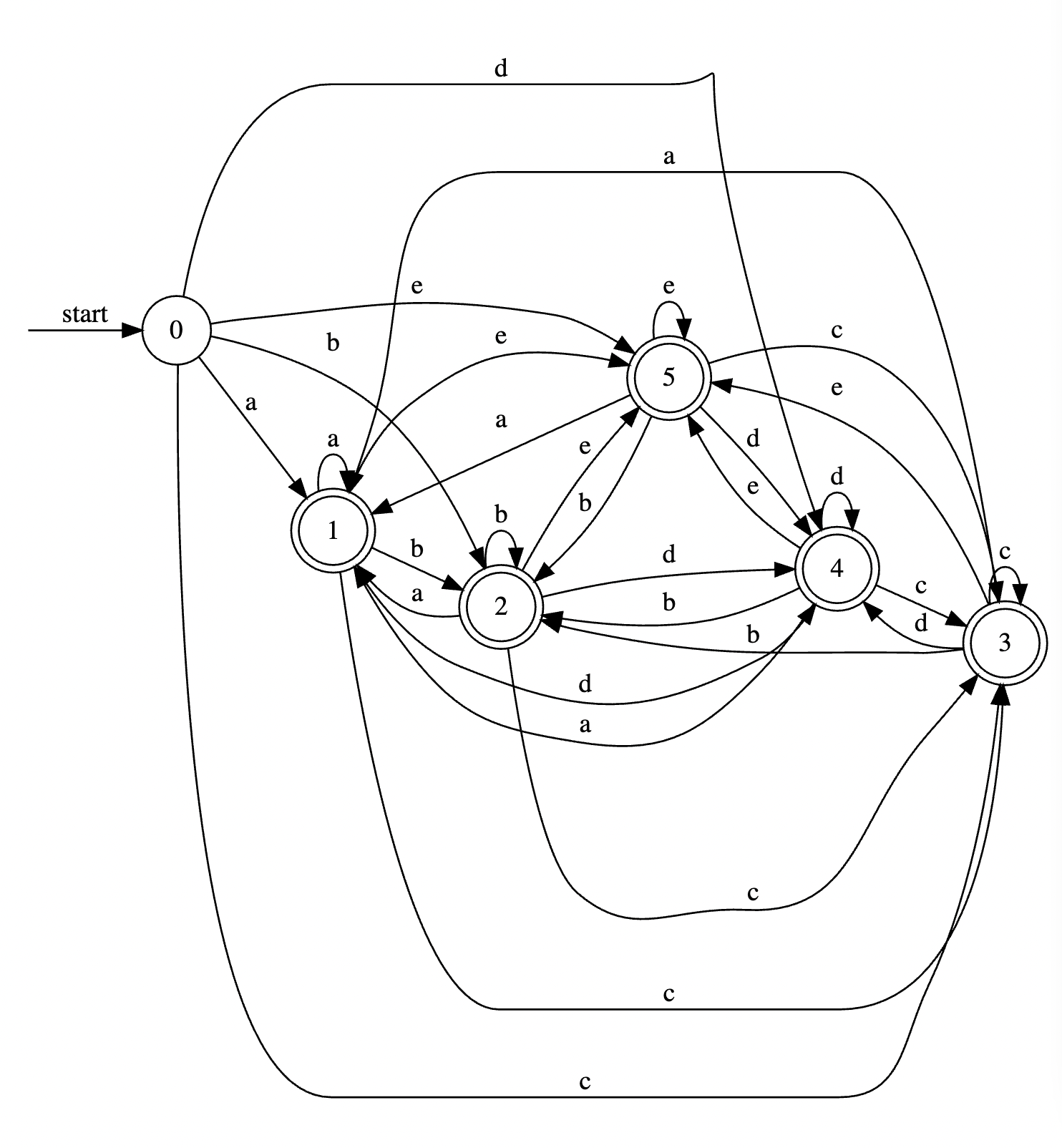
もう言うまでもないでしょう。[a-z]+ にするだけで 26 * 26 = 676 本の遷移が、[a-zA-Z0-9]+ にすると 3844 本の遷移が発生し、ちょっと遷移が複雑な正規表現を書くだけで、あっという間にメモリを食い尽くしてしまいます。なお上のグラフはこのページで描いたのですが、\w+ を DFA にコンパイルしようとすると落ちました。仕方ないですね。\w(a|b|c|d|e)+ くらいだと頑張ってくれますので、試してみてください。

結論としては、DFA への変換は理論上は常に可能ですが、現実的なリソースで DFA 変換が不可能な場合が多いので実用エンジンでの利用は限定的です。なので、いろいろな言語の正規表現エンジンは、それぞれ現実的な範囲で最適化をしながら、最悪のパターンで計算量が爆発する可能性を止むなしとしていることが多いです。

余談: Go の正規表現エンジンは O(mn)

色々な正規表現エンジンの実装の中で、Go の標準の正規表現エンジンの実装は面白いので紹介しておきましょう。

Go の正規表現エンジンも NFA ベースですが、Thompson’s construction と呼ばれる方法で NFA を構築しています。この方法で NFA を構築すると、一つの状態からの枝の広がりが必ず 2 本までに制限され、また常に右側（もしくは自分自身）に遷移し、既存の状態に戻らないことを保証しながら NFA を構築することが出来ます。

そしてそのような NFA に関しては、幅優先探索を行うことが可能になります。そうすると、正規表現の長さを m、入力文字を n として、最悪 O(mn) の計算量でゴールにたどり着けるかどうか（受理状態になるかどうか）を判定することが可能になります。具体的な実装はこのページで紹介されていますので、ぜひ見てみてください。

O(mn) は大変短く、現実的な入力においてはほぼ現実的な時間で終わります。入力文字が 300000 文字くらいで、やっと少し重いかな…と思う程度でしょうか

	r := regexp.MustCompile(`(.*){1,200}[bc]`)
	r.MatchString(strings.Repeat("a", 300000))

ではなぜこの方式を他の言語でも採用しないのか、というと、この実装だと一般的に利用される正規表現の検索で少し遅くなってしまうのです。特殊な状況で計算量が爆発しない代わりに、普段利用では少しコストがかかるという話です。これはどちらが優れているかという話ではなく、トレードオフです。Go なら、一般的な正規表現を多用する場合に深さ優先探索をしているパッケージを利用すればいいだけなので話は簡単ですね。

対策

さて実装が理解できたところで、対策です。主に JavaScript における対応策をご紹介します。

正規表現を使わない

正規表現を使わなければ、少なくとも ReDoS 対策は不要です。使わずに簡単に書けるなら使わないという選択肢が一番安全ですが、まあ極論ですね。

ツールで弾く

脆弱性が存在するかどうかを、人が正規表現を見て判断するのは難しいです。そういうものはツールに任せるに限ります。

• この recheck というサイトでは、正規表現を入力すると具体的にどのような入力に対して脆弱なのかを確認出来ます。Twitter で gfx さんに紹介して頂きました
• eslint-plugin-regexp を使ってチェック出来ます。ルールと Demo を Twitter で @omoteota さんに紹介して頂きました
• CodeQL のような分析ツールでも検知出来るらしいことを Twitter で @petamoriken さんに紹介して頂きました

ただし、ツールでの判定も 100% 正確というわけではない点に留意してください。本来は問題のない表現を問題視するかもしれませんし、問題のある表現を通してしまうかもしれません。

問題の少ない正規表現エンジンに切り替える

ReDoS の発生しにくい正規表現エンジンを利用する方法もあります。Yosuke Furukawa-san に教えていただいた re2-wasm は指数爆発が発生しないことを主張しておりますが、一方でこの re2-wasm は先読みや後方参照に対応していません。

新しい正規表現の l オプションを利用する

V8 で experimental で導入されている non-backtracking RegExp engine が利用可能であれば、それを使うのも良い判断になると思います。Twitter で @yapatta_prog さんに紹介して頂きました。

$ nvm use 16
Now using node v16.10.0 (npm v7.24.0)
$ node --enable-experimental-regexp-engine
Welcome to Node.js v16.10.0.
Type ".help" for more information.
> /(.*){1,20}[bc]/l.exec("a".repeat(25))
Uncaught:
SyntaxError: Invalid regular expression: /(.*){1,20}[bc]/: Cannot be executed in linear time

このような形で、l オプションをつけることで線形時間で実行出来ない正規表現を Syntax Error で弾いてくれます。線形時間で処理されることが保証されるので ReDoS は絶対に発生しません。これが正式に採用されたら嬉しいですね。具体的な話は上記の V8 のブログを参考にしてみてください。

運用で弾く

私は kazuho-san の指摘に賛成で、結局、バグなり何なりで無限ループが発生するリスクは ReDoS 以外でも普通にあるわけで、そういうリスクに対して個別対応ではなく運用で対応出来る体制を取るのが理想的だと思います。タイムアウトを設定して、落ちた場合にログで追える運用体制を作ることが出来れば、たいていのサービスにおいては仮に ReDoS が舞い込んでも即死級の問題になることは少ないでしょう。可能であれば運用でのカバーも検討したいところです。

まとめ

ReDoS は、基本的には言語の仕様によるものではなく、正規表現エンジンの実装に依存するものですから、基本的に「この言語だから安全」みたいなことは言えません。またエンジンによってどのような表現が得意でどのような表現が苦手かの差異もあり、一般論として「この表現なら駄目」「この表現なら大丈夫」と主張するのも難しいです。

本気で理解しようとすると奥の深い問題ではあるのですが、この問題の背後には正規表現と NFA / DFA の関係に始まるアルゴリズムの話があり、計算理論の入り口として大変に魅力的な題材なのです。オートマトンは大学レベルの話ですが、さわりでも知っておくと脆弱性の本質的な問題の理解に繋がります。強く興味をもった方は、これを入り口として計算理論の探求に入られると面白いかもしれません。

今回の記事では、オートマトンの基礎の基礎、ほんのさわりのみをお伝えしました。もっと深く知りたければ、例えば「計算理論の基礎」であるとか、いわゆるドラゴン・ブックであるとかで解説されていた記憶があります。リンク先は新装版ですが、私は両方とも初版で読んだので、内容が変わっていたらすみません。ドラゴンブックの方は古典の名著で個人的にも好きなのですが、読みにくい・わかりにくいとの評判も根強くあります。一方で計算理論の基礎はわかりやすく、読んだ時にとても感動した記憶があります（そもそもドラゴンブックはコンパイラの作り方の本であり計算理論の本ではないので、比較するのは適当ではないですが、どちらも好きな本なのでつい）。

当たり前ではあるのですが、我々が日々使っている正規表現やコンパイラなどは、計算理論の長い歴史に裏打ちされています。今回のように、ちょっとした計算量の話のすぐ裏側に横たわっているので、良いタイミングがあれば少し潜ってみると面白いと思います。

追記

Twitter で @Mi_Sawa さんから、Go の正規表現エンジンの計算量のミスの指摘を受けましたので記事を修正しました。修正点に関しては github をご確認ください。ご指摘ありがとうございました！