Special Thanks to @hagat and @teehah for reviewing my articles!
近年、WebGLに流行の兆しが出てきました。WebGLとは、ブラウザに何らプラグインをインストールすることなく、JavaScriptよりGPUを使用した3Dの表示を可能とする技術です。プラグインのインストールが必要ないとはいえ今までは対応ブラウザが少なくあまり実用的ではありませんでしたが、先日のiOS8で正式に対応されたことでモバイルブラウザにおいて対応率が跳ね上がり、スマートフォンにおいてブラウザベースで3Dのゲーム等を作れる可能性が急激に高まりました。
今回WebGL Advent Calendarの一環として、生WebGLで3Dのオブジェクトを表示するところまで挑戦してみます。WebGLにはthree.jsを始めとして有用なライブラリがたくさんあり、大抵の場合は適したライブラリを使用するほうが良いでしょう。しかし、ライブラリの背景を知らずに機能だけを使っているよりは、ライブラリ内部でどのような処理が行われているのかを理解している方が良いのは言うまでもありません。今回は基礎を知るために、生のWebGLを触ってみることにしました。
今回の記事の最終目的は、3DモデルをWebGLで表示することです。特に、プログラミング言語(JavaScript)はある程度得意だけれど3D技術はほとんどわからない、という方にとって有益な記事になれば幸いです。
準備
まず3Dのデータを用意します。探せば色々とあるのでしょうが、綺麗なモデルのデータがたくさんある Miku Miku Dance(以下MMD)の3Dデータを利用してみたいと思います。今回、まず最初にMMDの標準モデルである「あにまさ式ミク」と呼ばれるモデルを選びました。MMDのパッケージの中にある "初音ミク.pmd" です。

MMDのデータはPMD、PMX形式で配布されているので、まずはこれを人が読める形式であるOBJ形式に変換したいと思います。今回はオープンソースの3D編集ツールであるBlenderを使いました。このBlenderって奴はとにかく初見殺しで、エンジニアの人向けには「3Dの世界のvim」といえば伝わるでしょうか。自分のWinノートパソコン環境だと、視点の移動一つ出来なくて大変でした。自分は未だにさっぱり慣れていませんが、とりあえず困ったらスペースを押してコマンドを入力する、という方法で切り抜けています(Move ViewとかRotate Viewとか)。
Blenderの細かい使い方については割愛しますが、PMD形式は標準ではサポートされていないので、まずPMDのimportをサポートするプラグインをインストールし、それを使ってインポートします。確か自分が使ったのはこれだったと思いますが、読み込みができればどれを使っても大丈夫です。そして、importしたオブジェクトを標準でついているOBJ exporterでexportして完了です。
なお、MMDのモデルは当然ながらMMD専用なので、一部のモデルはMMDに特化しているためBlender等では崩れることがあります。例えば、有名な「Lat式ミク」をimportしたところ、(グロ画像・閲覧注意)大変なことになってしまいました。どうしてこうなるかの理由についてはこのサイトが詳しいです。
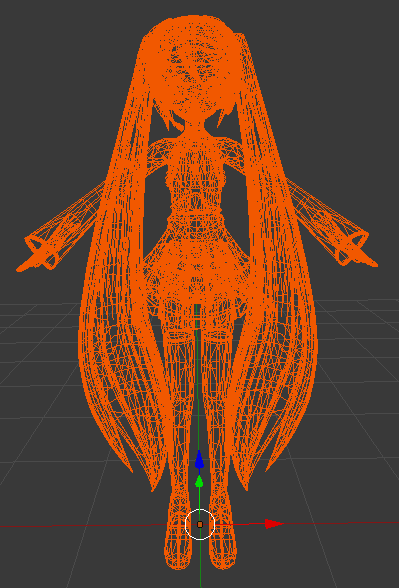
さて、上記の工程を経て、miku.obj、miku.mtl が生成されました。両方ともテキストファイルで、人間が中身を読むことが出来ます。それとmiku.mtlの中で定義されている eyeM2.bmp を加え、この3つのファイルが「あにまさ式ミク」を形作っていることになります。
ポリゴンを1枚表示する
さて、準備が整ったところで早速WebGLの世界に入っていきましょう。3Dのモデルは大量のポリゴン(3次元の座標を持った三角形)により構成されております(あにまさ式ミクの場合は22961枚です)。WebGLはポリゴンを大量に高速に描画することが出来るのが特徴です。というわけで、まずは1枚ポリゴンを書くことを目標にしましょう。
先にお伝えすると、ポリゴン1枚表示するために、かなりのコードが必要になります。しかし1枚ポリゴンさえ書いてしまえば、後はそれを何枚どのように書くかだけの話となるので、そこからの話はスイスイ進みます。ミクさんの表示目指して頑張りましょう!
初期化
まずは、とりあえず初期化するところだけでも書いたのがこちらです。
https://github.com/tkihira/webgl-miku-sample/tree/a1f307394fa5b3bbdfa05657c0affbbf4e1d9894
WebGLはパイプラインで構成されております。まずVertex Shader(以下VS)と呼ばれるプログラムに頂点データが入力として流し込まれ、VSは頂点データを描画の座標系(クリップ座標系)とその座標が持つデータに変換して出力します。次に、WebGL内の処理として、頂点データ同士を適切につなぎ合わせ(たいていは三角形でつなぎます)、その三角形の内部のデータを補間します(VSの出力データが色データだった場合は、グラデーションする感じですね)。最後にFragment Shader(以下FS)と呼ばれるプログラムが各ピクセルごとに呼ばれます。FSは補間されたデータを受け取り、それを出力する色画像に変換して出力します。
そして、VSとFSはユーザーがプログラムとして記述することが出来ます。GLSL(OpenGL Shading Language)と呼ばれるC言語風の言語で書きます。今回のコードではGLSLを適当に記述していますが、JavaScript側でindex.htmlに書いたGLSLを取得し、コンパイルし、ひとつのプログラムとしてリンクしているのが今回のコードです。リンクまでしかしていないのでエラーは出ませんが、このプログラムは初期化するだけで実際には何の出力もしません。
行列の効果
さて、行列は3Dプログラミングをする上で避けて通れません。具体的な行列の計算はただの足し算掛け算の羅列なのですが、その効果は大変便利なものです。というわけで、今回は「効果」だけを説明しちゃいます。行列について詳しく知っていることが望ましいのは言うまでもないですが、とりあえず効果さえ知っていればなんとかなります(断言)。
行列は簡単にいうと「座標変換」のデータです。例えば、建物のモデルとミクさんのモデルの高さが同じだった場合、建物のモデルを3倍くらいに大きくしたいなーと思うわけですが(ミクさん縮めるでもいいです)、そういう時どうすればいいでしょうか。モデルの頂点データが(x, y, z)と格納されているなら、すべてのデータを(x * 3, y * 3, z * 3)と三倍にしてしまえば良さそうです。では別に、ミクさんの位置をちょっとx方向に10だけ動かしたいな…と思ったとしましょう。その場合は(x + 10, y, z)にすれば良さそうですよね。
行列は、このような計算に最適なツールとなります。拡大縮小や平行移動だけでなく、回転などの表現も可能です。ある行列Mに対して、ベクトルvを掛ける(M * v)と、その掛け算の結果はベクトル(v')となり、v'ベクトルは回転などの座標変換された情報になります。さらに、行列同士を掛け算すると行列になるのですが、掛け算された結果の行列はそれぞれの効果を掛けあわせた効果を持つ行列となります。例えば移動の行列をT、回転の行列をR、拡大の行列をSだとすると、T * R * S と掛けあわせて出来た新しい行列Mは、「拡大して回転して移動する」というのを一括してやってくれる便利行列となるのです。
さて、前述したとおり、最終的にVSはクリップ座標系で出力する必要があるのですが、相当大雑把にいうとx, y, zを全部[-1, 1]の範囲の箱に入れる(その範囲外の場合は描画されなくなる)ということです。そして、その箱をZ軸沿いから眺めた絵が、出力される絵になるのです。かなりかいつまんで話していて、実際は違うのですが、イメージとしてはそういう感じです。
しかし実際のプログラムでは、自分の定義した三次元空間(世界座標系)に自由自在にモノを置いて、それを適当に眺めたいわけです。そういう時に活躍するのが上記の行列の効果になります。三次元の時には、frustum(錐台)と呼ばれる変換をよく使います。世界座標系の、錐台の中に入ったやつをぐにゃりと曲げて、クリップ座標系の箱の中にぴったりに入れる変換効果だと思ってください。
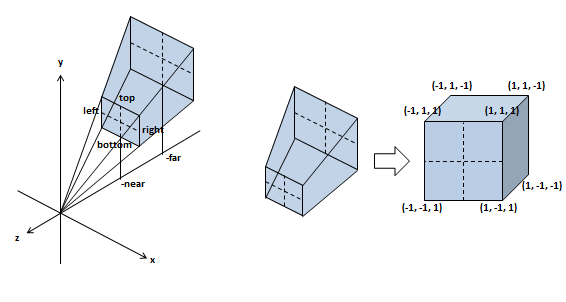
(正確には、クリップ座標系はWebGLの内部機構によりw要素で同次除算され、その結果が[-1,1]に正規化された正規化デバイス座標系になり、最終的に上記の変換が行われます。なので、frustum関数の生成する行列は、同次除算をおこなうと錐台が四角になるような良い感じの(x,y,z,w)を生成するような行列ということになります。詳しくは、座標系についてはこちら、frustumの変換に関してはこちらを参照してください)
今回のプログラムでは、ポリゴンをそのfrustumの中に入るように平行移動する行列(translate)と、せっかくなのでポリゴンをクルクル回転させる行列(rotate)を使っています。こういった行列を生成するライブラリとして、今回はglMatrixを利用しました。WebGLを使う際にはこの行列ライブラリが多分いちばんいいのではないかと思っています。glMatrixはソースも綺麗なので、中身を読んでみると行列がどのように生成されているのかわかると思います。
WebGLへのデータの送信
WebGLへのデータの送信までを行うコードはこちらです。
https://github.com/tkihira/webgl-miku-sample/tree/ccc2addef05e407e145b98f55d270ace0e9c8c06
新しく、loadBuffer関数を用意しています。ここでは、唯一のポリゴンである三角形のデータと、その三角形の法線ベクトルを用意しました。三角形は、今回は3つの頂点をそのまま座標で指定しました。XYZ座標順に入っているので、(-0.5, -0.5)-(0.5, -0.5)-(0.5, 0.5)(Z座標はゼロ)というXY平面上の直角二等辺三角形です。そして法線ベクトルもついでに用意しました。法線というのは、ある面に垂直な方向ベクトルを示すデータです。その三角形が曲面の一部だった、という場合は3つの頂点でバラバラの法線を持つことになるのですが、今回は全部同じ方向(0, 0, 1)、Z軸方向を向いてもらいました。
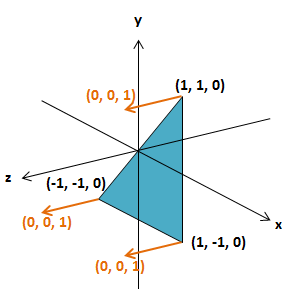
bindBufferで今から扱うバッファを指定し、そこにデータを流し込んでいます。WebGLで使うデータはTyped Arrayで行われます。JSの配列をFloat32Arrayに変換して、bufferDataで流し込めばOKです。
さて、では描画のところを見ましょう。まず最初に、先ほどの錐台(frustum)の行列と、平行移動&回転の行列を用意しています。そしてそれをuniformという形式でVSに渡しています。
プログラムからVS・FS、VSからFSにデータを送る方法は、大きく3つあります。一つがuniformで、これはプログラムから定数値(頂点によって変わらない値)をVSもしくはFSに送る場合に使います。今回は、行列は頂点によって変わるものではないので、uniformで定数値として送ってしまいます。次に、プログラムから頂点ごとのデータを送る時に使われるのがattributeです。今回は、頂点ごとのデータvertexと、法線データnormalをattributeで送っています。最後に、VSからFSにデータを送るときに使われるのがvaryingです。これは上記でいったVSでの出力、FSでの入力の関係です。例えばvaryingで頂点ごとの色データを渡すと、WebGL機構の内部で補間(グラデーション)が行われ、FSではピクセル単位で色データを受け取ることになります。VSとFSのvaryingの変数名は一致しています。
今回はプログラムから行列をuniformで送り、頂点データと法線データをattributeで送ります。その処理をしているのがdrawFrameのところです。まず錐台を適当に設定し、三角形がその中に入るように平行移動し、ついでに回転軸(0, 1, 0)で適当に回転する行列を作成しています。そしてそれらをuniformでVSに送る準備をしています。頂点データ・法線データもそれぞれattributeで送る準備をし(頂点データ数は3個ずつと設定しています)、最後にdrawArraysで3頂点分のデータをWebGLに流し込んで完了です。
Vertex ShaderとFragment Shader
では最後に、VSとFSで何をやっているのか見てみましょう。
まずVSですが、受け取った錐台の行列と移動回転の行列を頂点データに掛けあわせ、(-1,-1,-1)-(1,1,1)の箱の中の座標に変換しています(前述の通り、正確にはw要素による同次除算の結果そのようになるクリッピング座標系に変換しています)。その座標をWebGLに対してgl_Positionという予約変数に入れることで伝えます。また、FSでは傾きに応じて明暗をつけたいので、e_normalというvaryingで頂点ごとの法線データを渡しています。法線データは世界座標系での値がほしいので、移動回転の行列のみと掛けあわせて渡します。
これでWebGLの内部機構が、頂点の情報(三角形を構成する三つの頂点の座標変換の結果のウィンドウ座標)からどこのピクセルに描画されるのかを確認し、その対象全ピクセルに対してFSが呼ばれることになります。
FSでは、まずそのピクセルでの法線データをvaryingで受け取り(補間される際に正規化が狂っている可能性があるので正規化しています)、光源のベクトルを適当に(0, 0, 1)と設定し、それと法線との内積(dot)を取ることでその点の明るさを(勝手に)求めています。ベクトルの内積は、2つのベクトルが同じ方向を向いていれば向いているほど大きな値になります。面(法線ベクトル)が光の方向を向いてるほど明るくするのに丁度良いので、それを利用して光の明るさを便宜的に求めています。
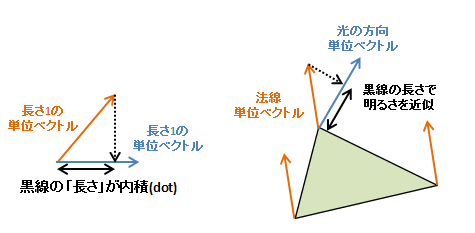
光については、とりあえず今回はそれっぽく見えたら良し、という認識でやっています。そしてその内積した結果をgl_FragColorという予約変数に代入することで、そのピクセルがその色で描画されてCanvasに表示されることになります。
結果
想定したとおりに三角形が1枚舞っています。たかがポリゴン1枚を書くのがこんなに大変だなんて…!と思われた方が多いかもしれません。しかし、ミクさんもいわばただのポリゴンの集まりなので、実はこれでもうほぼミクさんが描けたも同然なんです。長くなったので次の記事に移りますが、この先あまりに簡単にミクさんの全体像が表示できるので、きっとびっくりされると思います。
次の記事はこちら→ 生WebGL入門:初音ミクの美麗3Dモデルを表示する(中編)