2023 年、あけましておめでとうございます!私は元旦に次のようなオリジナル・パズルを出しました。
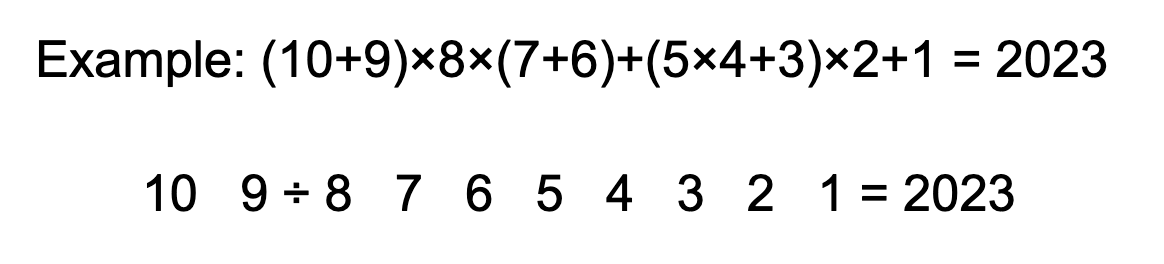
上の例のように、数字の合間に四則演算(+−×÷)や括弧を入れることで、2023 を作ってください。
- 数字の間に必ず演算子を 1 つ入れてください
- ただし 9 と 8 の間には既に ÷ が入っています
- 括弧は複数重ねて使用できます
- 10×(-9 ÷ 8) のようなマイナス記号の使用は禁止です
オリジナルツイートはこちらです。この記事では、JavaScript によるこのクイズの解き方をご紹介します。
括弧の数式をプログラムで扱うには
さて、この問題の一番厄介な点は、括弧の絡む数式をプログラムで処理するという点ではないかと思います。この記事でもそこを重点的に解説したいと思います。
中置記法
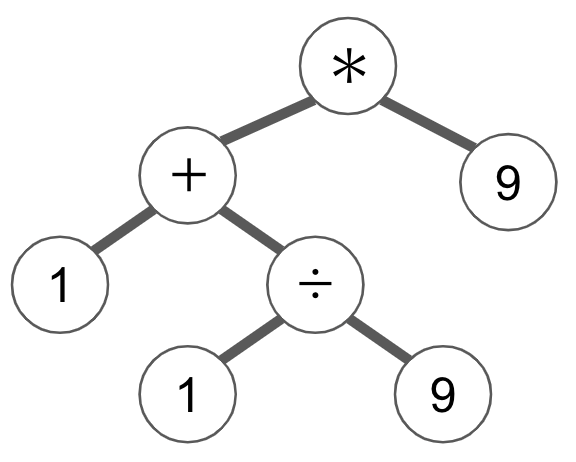
まず、我々が日常的に使っている数式は、いわゆる「中置記法」と呼ばれる記法です。例えば
(1 + 1 / 9) * 9
のように、数字と数字の間に演算子が入ります。また、演算子の優先順位付けが定義されており、たとえば掛け算は足し算よりも優先して計算されるため、恣意的に順位をつけるためには括弧を利用しなければいけません。
なお、数式は二分木として表現することが出来ます。すべてのリーフノードは数字となり、内部ノードは演算子になります。上記の数式を二分木で表現した図が次の通りです
逆ポーランド記法
数式の二分木を、括弧を使わずに表現する際に広く使われているのが「逆ポーランド記法(Reverse Polish Notation)」とよばれる記法です。頭文字をとって RPN と略されることが多いです。逆ポーランド記法では、あらかじめ演算する数字を書いておき、最後に演算子を記述する形になります。
例えば、上記の (1 + 1 / 9) * 9 を逆ポーランド記法で書くと、
1 1 9 / + 9 *
となります。直訳すると、「1 に、1 を 9 で割った結果を足して、それに 9 を掛ける」という風に読めます。
逆ポーランド記法だと、中置記法のように数字と数字の間に必ず演算子が入るわけではないので、数字の間に区切り(今回はスペース)が必要になります。一方で、括弧を必要とせずに数式を記述出来ます。逆ポーランド記法で記述された数式には、次の特徴があります。
- 数字の数は、演算子の数より必ず 1 つ多い
- 数式の途中において、数字の数は演算子の数より常に 1 つ以上多い
余談ですが、慣れると記述しやすいと感じる人が多く、例えばヒューレット・パッカード社の関数電卓には RPN モードが搭載されており、一部の界隈では大変好評でした。私も逆ポーランド記法目的でヒューレット・パッカード社の関数電卓(HP-28C)を愛用していたクチです。
逆ポーランド記法のコンピュータによる処理
逆ポーランド記法は、コンピュータによる計算と非常に相性が良いので、数式を扱う必要のあるプログラムではよく使われます。コンピュータでは次のように処理されます。
- 空のスタックを用意し、数式を前から読み込む
- 数字が出てきたら、その数字をスタックに格納する
- 演算子が出てきたら、スタックから 2 つ値を取り出し、それらを演算した結果をスタックに格納する
- 数式が終わると必ずスタックに 1 つ数字が残っているはずなので、その数字が演算結果となる
実は、これはいわゆる「スタックマシン」と同じ演算になります。例えば Java や WebAssembly などのスタックマシン言語においては、バイナリレベルでは大体同じ様な構造を持っています。
パズルを解く戦略
私は、今回のパズルを解く戦略を次のように定めました
- まず逆ポーランド記法で数式を全通り生成する
- その数式を演算して、解が 2023 になるかどうか確認する
- 逆ポーランド記法を中置記法で書き下す
それぞれについて解説します。
全通りの数式の生成
今回の問題では 9 と 8 の間に割り算が入っているのですが、とりあえずそれを無視して全通りの数式を出すことを考えてみましょう。
let counter = 0;
const traverse = (expr, number, opes, nums) => {
const opCharList = [..."n+-*/"];
if (number === 0 && nums - opes === 1) {
counter++;
// solve(expr)
}
for (const op of opCharList) {
if (op === 'n') {
if (number > 0) {
expr.push(number);
if (traverse(expr, number - 1, opes, nums + 1)) {
return true;
}
expr.pop();
}
} else {
if (nums - opes >= 2) {
expr.push(op);
if (traverse(expr, number, opes + 1, nums)) {
return true;
}
expr.pop();
}
}
}
};
traverse([], 10, 0, 0);
console.log({counter});
何も考えずに再帰で書いています。簡単に解説すると、
- expr は生成途中の数式を配列で管理しています。number は次に登場する数字、opes は今までの演算子の数、nums は今までの数字の数です
- 再帰関数では、expr 配列の最後に「数字」もしくは「演算子」を 1 つ追加して、再度自分自身を呼びます
- 終了条件は、number がゼロ(もう数字が登場しない)、かつ今までの数字の数と演算子の数の差が 1 になった場合です
なお、このプログラムを実行すると、手元のコンピュータでは 2 分 20 秒かかり、counter が 1,274,544,128 になりました。
割り算を考慮して生成
ちょっと数が大きすぎるので、9 と 8 の間の割り算を考慮することにしましょう。割り算は 9 と 8 の間に入れたいのですが、(9 / 8) だけではなくて、例えば 9 / (8 - 7) のような形も存在することに気をつけましょう。
これを実現するには、逆ポーランド記法の特性を考えると、「8 の数字が出た後、数字と演算子の数が一致していた場合」の演算子を割り算に固定してしまえば良いことになります。
9 8 /: この場合、8 の数字が出た後の数字と演算子の数は共にゼロになります。中置記法だと9 / 8になります9 8 7 - /: この場合、8 の数字が出た後の数字と演算子の数は共に 1 になります。中置記法だと9 / (8 - 7)になります9 8 7 6 - 5 + * /: この場合、8 の数字が出た後の数字と演算子の数は共に 3 になります。中置記法だと9 / (8 * ((7 - 6) + 5))になります
それを考慮してコードを書くと、次のような感じになります。
let counter = 0;
const traverse = (expr, number, opes, nums, eightDepth) => {
const opCharList = [..."n+-*/"];
if (number === 0 && nums - opes === 1) {
counter++;
// solve(expr)
}
for (const op of opCharList) {
if (op === 'n') {
if (number > 0) {
expr.push(number);
if (traverse(expr, number - 1, opes, nums + 1, number === 8 ? 0 : eightDepth < 0 ? eightDepth : eightDepth + 1)) {
return true;
}
expr.pop();
}
} else {
if (nums - opes >= 2) {
if (eightDepth === 0 && op !== '/') {
continue;
}
expr.push(op);
if (traverse(expr, number, opes + 1, nums, eightDepth - 1)) {
return true;
}
expr.pop();
}
}
}
};
traverse([], 10, 0, 0, -1);
console.log({counter});
手元では 37 秒、counter は 318,636,032 でした。大体 1/4 程度まで探索量を減らせました。
逆ポーランド記法の数式の計算
さて、では上記でコメントアウトされていた solve 関数を作ってみましょう。実装は非常に簡単です。
const solve = (expr) => {
const stack = [];
for (const c of expr) {
switch (c) {
case '+': stack.push(stack.pop() + stack.pop()); break;
case '-': stack.push(-stack.pop() + stack.pop()); break;
case '*': stack.push(stack.pop() * stack.pop()); break;
case '/': stack.push(1 / stack.pop() * stack.pop()); break;
default: stack.push(Number(c)); break;
}
}
const result = stack.pop();
if (Math.abs(result - 2023) < 0.001) {
// prettyPrint(expr);
console.log(expr.join());
}
};
数値が来たら stack に push して、演算子が来たら stack から取り出して計算し、演算結果を stack に push しています。最後は必ず stack に 1 つ答えが残っているので、それを 2023 と比較しています。stack には右辺値、左辺値の順番で積まれているので、引き算と割り算ではまず右辺値を扱う必要があることに気をつけましょう。
また、result には浮動小数点演算による丸め誤差が含まれている可能性があるので、epsilon を 0.001 として比較しています。数式的に桁落ちもないので私はこれで十分だと判断しましたが、正確に計算するためには仮想分数を自前で管理する必要があります。特に競プロ界隈ではこういった誤差を適当に処理することを許さない問題が多いので気をつけましょう。
このプログラムを実行した結果、手元の計算では 530 行の出力を 3 分 33 秒で得られました。Twitter 等では、この結果と同じように全件を 530 件として出していらっしゃる方が多いです。
逆ポーランド記法から中置記法への変換
最後に、この結果を中置記法に変換し、人間に読みやすくしてみましょう。何も考えずに変換すると、次のようなコードになるでしょう。
const prettyPrint = (expr) => {
const stack = [];
for (const c of expr) {
switch (c) {
case '+': case '-': case '*': case '/':
const r = stack.pop();
const l = stack.pop();
stack.push(`(${l}${c}${r})`)
break;
default: stack.push(Number(c));
}
}
console.log(stack.pop());
};
とにかく優先順位を考えなくてすむように、すべての項に括弧を付けた出力です。これでも良いのですが、例えば次の出力は中置記法においては同一視したいところですよね。
(((((10+(((9/8)+7)*(6*5)))*4)-3)*2)-1)(((((10+((((9/8)+7)*6)*5))*4)-3)*2)-1)
なので、不要な括弧を除去するようにしましょう。そして、重複する結果を出力しないようにします。コードは次のような形になります。
const prettyPrintLog = {};
const prettyPrint = (expr) => {
const stack = [];
for (const c of expr) {
switch (c) {
case '+': {
const r = stack.pop();
const l = stack.pop();
stack.push({ str: l.str + c + r.str, priority: 3 });
break;
}
case '-': {
const r = stack.pop();
const l = stack.pop();
if (r.priority < 3) {
stack.push({ str: l.str + c + r.str, priority: 3 });
} else {
stack.push({ str: l.str + c + '(' + r.str + ')', priority: 3 });
}
break;
}
case '*': {
const r = stack.pop();
const l = stack.pop();
const rStr = r.priority === 3 ? `(${r.str})` : r.str;
const lStr = l.priority === 3 ? `(${l.str})` : l.str;
stack.push({ str: lStr + c + rStr, priority: 2 });
break;
}
case '/': {
const r = stack.pop();
const l = stack.pop();
const rStr = r.priority >= 2 ? `(${r.str})` : r.str;
const lStr = l.priority === 3 ? `(${l.str})` : l.str;
stack.push({ str: lStr + c + rStr, priority: 2 });
break;
}
default:
stack.push({ str: c, priority: 1 });
}
}
const output = stack.pop().str;
if (!prettyPrintLog[output]) {
prettyPrintLog[output] = true;
console.log(output);
}
};
優先度を、数字: 1、掛け算・割り算: 2、足し算・引き算: 3 と規定し、それに従った出力をしています。このコードは、先程の結果を次のように同じ形で出力します。
((10+(9/8+7)*6*5)*4-3)*2-1
このコードを手元のコンピュータで実行すると、3 分 37 秒で 81 行の出力になりました。中置記法ならば、全件で 81 件あると言えそうです。
ここまでのコードと出力結果を、gist に用意しました。参考にしてみてください。
https://gist.github.com/tkihira/e27ba639de5be545f79b8c3decead68d
余談: JavaScript で手作業最適化
ところで、このコードを JavaScript で手作業で最適化を施したらどれくらい速くなるでしょうか。
- Stack の push/pop は重いので、配列を直接扱う
- 配列の中に数字と文字列が両方入らないように、演算子をマイナスで表現する
- その他細かい調整
アルゴリズムは一切変えていませんが、手元で実行すると 27 秒でした。8 倍の高速化です。
https://gist.github.com/tkihira/5d2add1e73019382bbcc63085c8cf527
10 年以上前はこのような高速化の効果が絶大だったのですが、最近はあまり必要ではありません。今回はあまりに無駄の多いコードだったので大きな効果が見えますが、普段のコーディングでこういった高速化が必要になることはあまりないでしょう。プロダクションでこのような探索コードを書く場合は、そもそも JavaScript を選ばないでしょうしね。
余談: 宣伝
私は大学生の時に共著で書いたアルゴリズム本で、逆ポーランド記法についてテンパズルを例に解説しています。かなり古い本で C や Java を前提に書かれているのですが、もし図書館などで出会いがあれば参考にしていただければ嬉しいです!